Spherical kinematic mount for a Fizeau interferometer

Manual kinematic mounts are used to orient optical components in one or more DOFs using micrometer heads. Often 2 DOF lateral mounts move an end-effector in a plane perpendicular to the optical axis. On the other hand, spherical mounts like stacked goniometer stages can manipulate optics about a fixed point on the optical axis, also known as the remote center of rotation. However, for measuring optical aberrations in lenses using a Fizeau interferometer an adjustable remote center of rotation is desired. At some point in the optical path, the interferometers laser beam is reflected back towards a CCD sensor using a return optic. This return optic should be manipulated in a spherical motion about a remote center of rotation on the optical axis. Depending on the focal length of the lens under the distance from the return optic to the remote center of rotation should be adjusted to minimize errors introduced during the calibration of the return optic.

The proposed design, shown in Figure 1 in 2D, consist of three flexure-based legs that connect to the end-effector in a trapezoidal manner. The support lines of these three legs intersect in a common point, allowing for a spherical movement of the end-effector around this point. A radial displacement of the base connections of the legs result in the desired shift of the RCR along the centre-line of the mechanism.

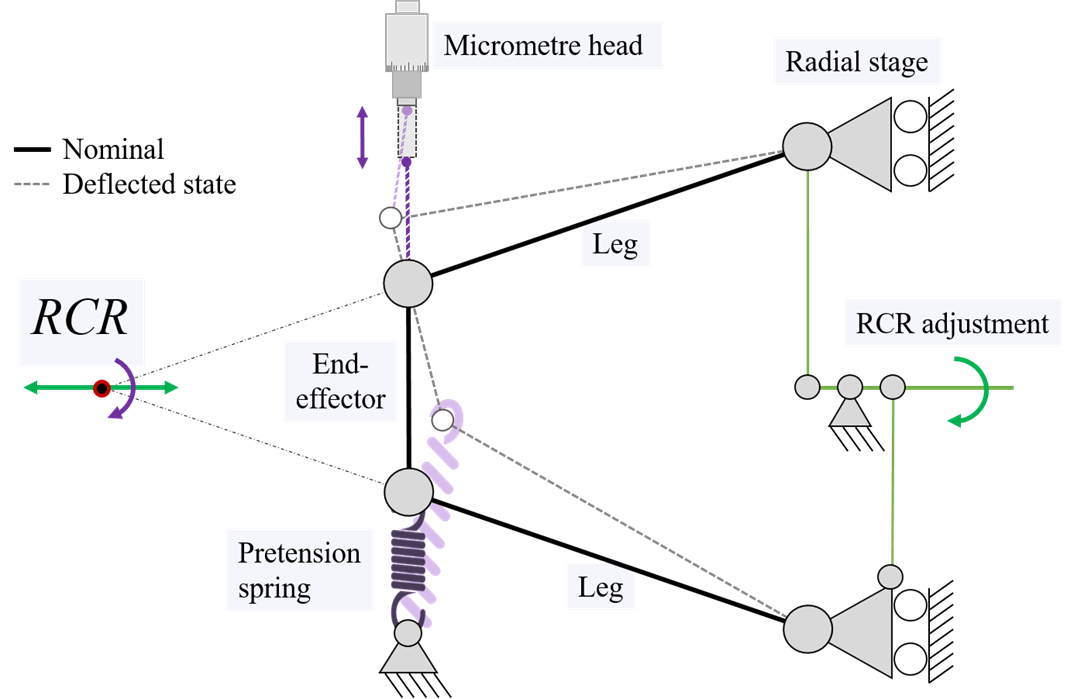
Figure 1, The working principle of the isosceles (legs with equal leg length) trapezoidal mechanism (in 2D) with an adjustable remote centre of rotation. By pulling the end-effector towards the Micrometre head, the end-effector is deflected about the RCR. Varying the orientation of the legs with the radial stages changes the RCR distance.

In order to make the legs of the trapezoidal mechanism flexure based, new developed flexure-based joints are integrated into the joints of the trapezoidal mechanism. These multi-DOF flexure joints consist of a cartwheel hinge of which the rotation axis intersects perpendicularly with the rotation axis provided by a leafspring pair, as shown in Figure 2. The leafspring pair is in one plane, and is short to mainly introduce one DOF with some range of motion. The torsion rotation is relatively stiff for a DOF and compliant for a constraint, therefore it lowers potential internal stress resulting from overconstraining, but it does not introduce unwanted parasitic internal vibration modes. Each leg with two spherical joints at their extremity therefore acts as reinforced wire-flexure that makes up the legs of a spatial isosceles trapezoidal structure, shown in Figure 3. Parallel flexure guides accommodates the radial movement of the base connection points of the legs for the remote center of rotation adjustment. A spiral guide synchronizes the separation of the three legs. By rotating the spiral at the back of the mechanism, the remote center of rotation distance can be adjusted from infinity (lateral movement only) to 45mm in front of end-effector shown.

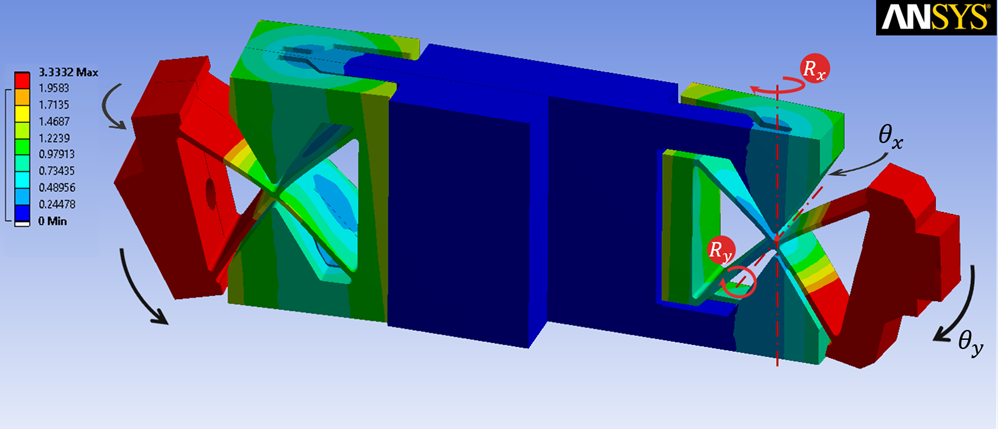
Figure 2. Simulated deformation plot of one of the legs in deflected state, with partial section view on the right-hand side. This 3D printed part uses two novel flexure based spherical joints. Ry- rotation has an angular range of 30 degrees. Rx- rotation has a range of 5 degrees. The unused space around the cartwheel hinge flexure is used by a notch type flexure to make the joints very compact.

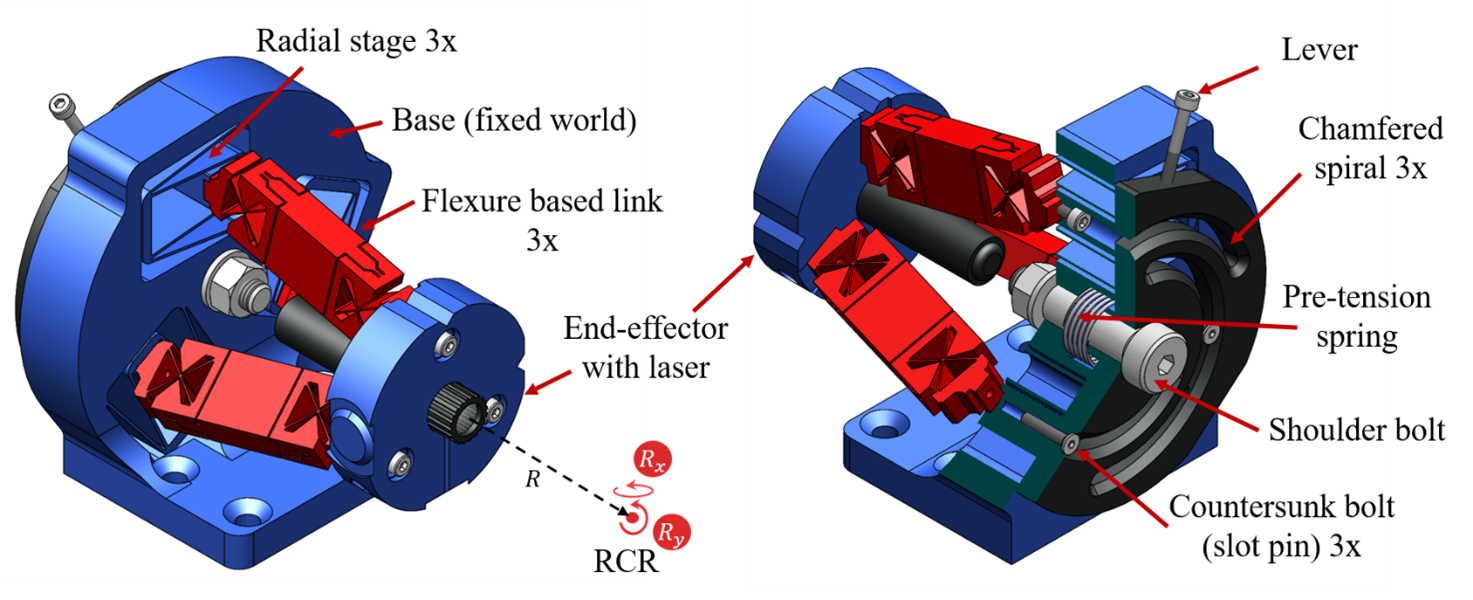
Figure 3. A 3D printed functional model of the spherical mechanism with adjustable remote center of rotation with legs in parallel (left) and converging (right) configuration. The legs are red, the spiral guide is black and the base and end-effector holding a laser pointer is blue. Left: mechanism rotates about the remote center of rotation at infinity. Right: Leg orientations are readjusted to rotate about RCR 45 mm in front of end-effector.

References 

[1] Koen J. Smelt , Jan J. de Jong , Coen A. Blok , and  Dannis M. Brouwer, Optomechanical spherical manipulator with an adjustable center or rotation, Proc. of the 35th annual meeting of the American Society for Precision Engineering, virtual meeting, October, 2020. 

Development 

Koen Smelt, Coen Blok, Demcon; Jan de Jong & Dannis Brouwer, University of Twente (2020)