1.3 Principles of thermal deformation
The coefficient of thermal expansion describes how the size of an object changes with a change in temperature. For solid materials with a significant length, an estimate of the amount...
The coefficient of thermal expansion describes how the size of an object changes with a change in temperature. For solid materials with a significant length, an estimate of the amount of thermal expansion can be described by the ratio ΔL / Linitial or linear strain:

where ΔL / Linitial [-] is the ratio of thermal strain, Linitial [m] is the initial length before the change of temperature and Lfinal [m] is the final length recorded after the change of temperature. The total strain is a combination of mechanical and thermal strain.
For most solids, thermal expansion scales linear with temperature difference:
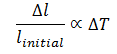
where ΔT is the temperature difference [K]. Thus, the change in strain can be estimated by:
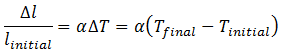
where α [K-1] is the coefficient of thermal expansion (CTE) in inverse Kelvin, Tfinal the final temperature [°C] or [K] and Tinitial [°C] or [K] the initial temperature and ΔT [°C] or [K] is the difference of the temperature between the two recorded strains.
Three principles can be distinguished. These principles are described for a plate in the xy-plane (for example a machine part) with length Lx in x-direction, which is shown in Figure 1.
- Longitudinal translation ∆Lx: in case of a uniform temperature change and/or gradient in x-direction (Gx), the beam will expand in axial (x) direction. The translation ∆Lx (x) is then the integrated sum of expansions of infinite small lengths dx:

- Rotation β: a temperature gradient in y-direction (Gy) introduces a local rotation dβ(x) around the z-axis caused by different expansions dLx at different heights y1 and y2. The rotation dβ(x) is obtained by integrating all local rotations dβ(x) over x:
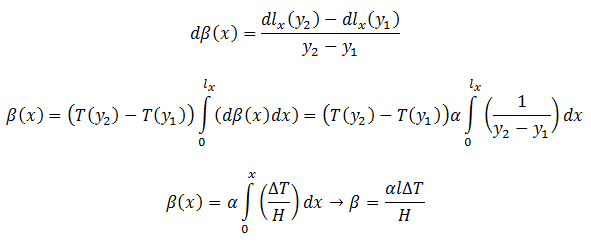
- Transversal translation caused by rotation f : a temperature gradient in y-direction (Gy) also causes a translation ∆y in the (negative) y-direction. This transversal translation can be calculated by integration rotation β over length Lx:
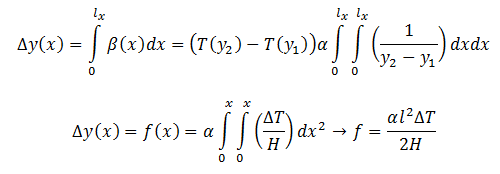
The shortening in y-direction introduced by the rotation β is a second order effect. For rotation, shortening ∆y=Linital (1-cos(α) ), for α is 0.1 mrad, ∆y=5∙10-9 ∙ Linitial.
It must be noted that material properties for most materials change as a function of temperature, which must be taken into account for e.g. cryogenic applications.
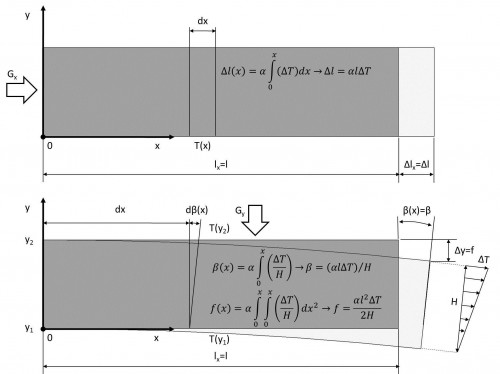
Figure 1: Deformations caused by expansions (or contractions)
Links:
