1.1 Temperature, heat and heat capacity
Any object contains a certain amount of thermal energy. Thermal energy is the energy contained in the kinetic energy of the random motion of molecules in a body on a macroscopic level. Of course, the molecules of a body in motion also have a kinetic energy, but this is not randomized, therefore it is not thermal energy.
Temperature is a measure of the averaged kinetic energy of the random particle motion. Again, averaged is a key word here. Only a large amount of particles together can have a temperature. The temperature property is important, because it always seeks an equilibrium. A body with a temperature gradient will always settle to a certain uniform equilibrium temperature in time, when no heat is exchanged with it’s environment. This occurs by the flow of heat within the body from warmer towards colder parts. Heat is best described as the transfer of thermal energy from one place to another. In fact, heat only exists as a flow of energy. If the flow stops, there is no heat.
Altering the temperature of an object requires a heat flow. As thermal energy flows into the object, its temperature will rise. The amount of energy (units: Joules [J] ) required to raise the temperature of the object by e.g. 1 Kelvin is called the object’s heat capacity (units: Joules per Kelvin [J/K]). The heat capacity of an object depends on its mass [kg] and the specific heat capacity of material. Every material has a certain specific heat capacity. This is the heat capacity [J/K] of one kilogram of the material. Specific heat capacity is a physical property of a material, measured in [J/(kg·K)].
| Name | Symbol | Units | Description |
| Heat | Q | J (joules) | Transfer of kinetic energy of molecules. Energy is always transferred from hot to cold. |
| Heat transfer rate | Q’ | W (Watts) | Rate at which energy is transferred. Sometimes called power (P) |
| Thermal energy | U | J (joules) | Energy contained in the kinetic energy of the random motion of the molecules of a body on a macroscopic level. |
| Heat Flux | q | W/m2 | Amount of heat transferred per unit area. |
| Temperature | T | K (Kelvin) | Property that is related to the average kinetic energy of molecules. Strives for equilibrium. |
| Specific heat capacity | c | J/(kg-K) | Material property: Amount of heat needed to raise 1 kg of a substance in temperature by 1 Kelvin |
| Heat capacity | C | J/K | Amount of heat needed to raise the temperature of a certain body by 1 Kelvin |
The table above lists the quantities, symbols and units that have been discussed up to now. Note that heat is described as an amount of thermal energy that is transferred (a certain number of Joules [J]). The energy transfer occurs at a certain rate (heat transfer rate), or a certain amount of Joules per second [J/s]. One Joule per seconds equal to 1 Watt [W].
Each of these physical quantities has a symbol, such as Q’ for heat transfer rate. A physical quantity can be measured in certain units. For example, the quantity Q’ is measured in the units of Watts [W].
Example 1
This is an example of a simple heating calculation. An aluminum part with a mass of 300g and a uniform temperature of 293K (about 20C) is heated uniformly for 30 seconds at a heat transfer rate of 10 W
| Mass: M=0.3 kg Temperature: 293 K Heating power: 10 W Heating time: 30 s Specific heat of Al: c = 897 J/kg K | Heat transfer rate: Q’ = 10 W Part heat capacity: C = c M = 269 J/K Temp change rate: dT/dt = Q’ / C = 0.037 K/s Total heat transfer: Q = Q’ * 30s = 300 J Total temp change: ΔT = Q / C = 1.11 K Temperature after heat transfer: T = T0 + ΔT = 294.11 K |  |
If we look up the specific heat capacity of aluminum, we’ll find it’s about 897 J/(kg·K). Therefore, the 300 grams part has a heat capacity of 269 J/K. In other words, for 269 joules of thermal energy we put into the part, its temperature will rise by 1 degree.
By heating it at a rate of 10W, for 30 seconds, we input 10J/s * 30s = 300 Joules of energy. The part’s temperature will rise (300 J)/(269 J/K)= 1.11 K. After the heat transfer, the part’s temperature is 294.11K. Since this occurs in 30 s, the rate of temperature change is 0.037 K/s.
Example 2
The same aluminum part as before, at 293K is brought into thermal contact with another part made of copper, with a mass of 100g, at a temperature of 303K. The heat capacities are 269 J/K and 38.5 J/K, respectively.
When the parts are brought into contact, heat will flow from warm to cold (copper part to aluminum part) until the temperatures are in equilibrium. What is the final, equilibrium temperature?
| Two separate parts have different heat capacities and temperatures Specific heat of aluminum: cAl = 897 J/kg K Heat capacity of part A: CA = cAl MA = 269 J/K Specific heat of copper: CCu = 385 J/kg K Heat Capacity of part B: CB = cCu MB = 38.5 J/K | 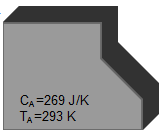 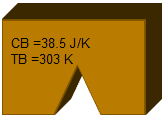 | Part A Material: Al Mass: 0.3 kg Temperature: 293 K Part B Material: Cu Mass: 0.1 kg Temperature: 303 K |
We know that an amount of heat (Joules) will flow from copper to aluminum. The amount that flows into the aluminum (Q) is the same amount that flows out of the copper (-Q). This will cause a temperature change of ΔT=Q/C and a final temperature of Teq= T+ ΔT for each part (as in the previous example). Since the final equilibrium temperatures are each part must be equal, we have two equations and two unkowns (Teq and Q). Solving the system of equations gives the answer.
| Temperature change: ΔT = Q / C ΔTA = +Q / CA ΔTB = -Q / CB Equilibrium temperatures: Teq= TA + ΔTA = TA + Q / CA Teq= TB + ΔTB = TB – Q / CB Teq= 294.25 K Q = 337 J | 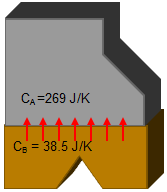 |
The assembly reaches an equilibrium temperature of 294.25 K, and 337 J of heat energy is transferred in the process.
