Chapter 2 - Design using flexures
Chapter 3 - Design for static stiffness
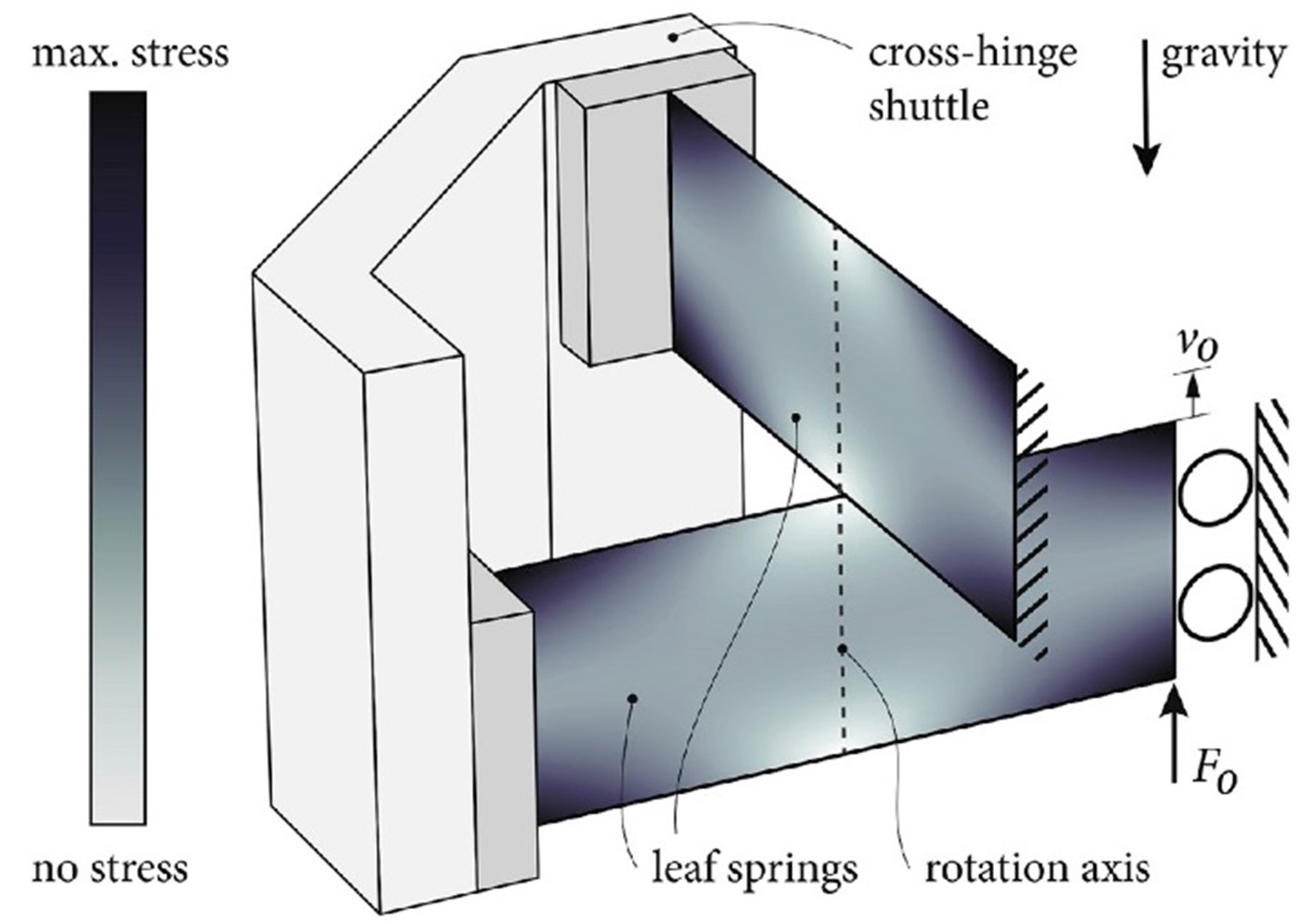
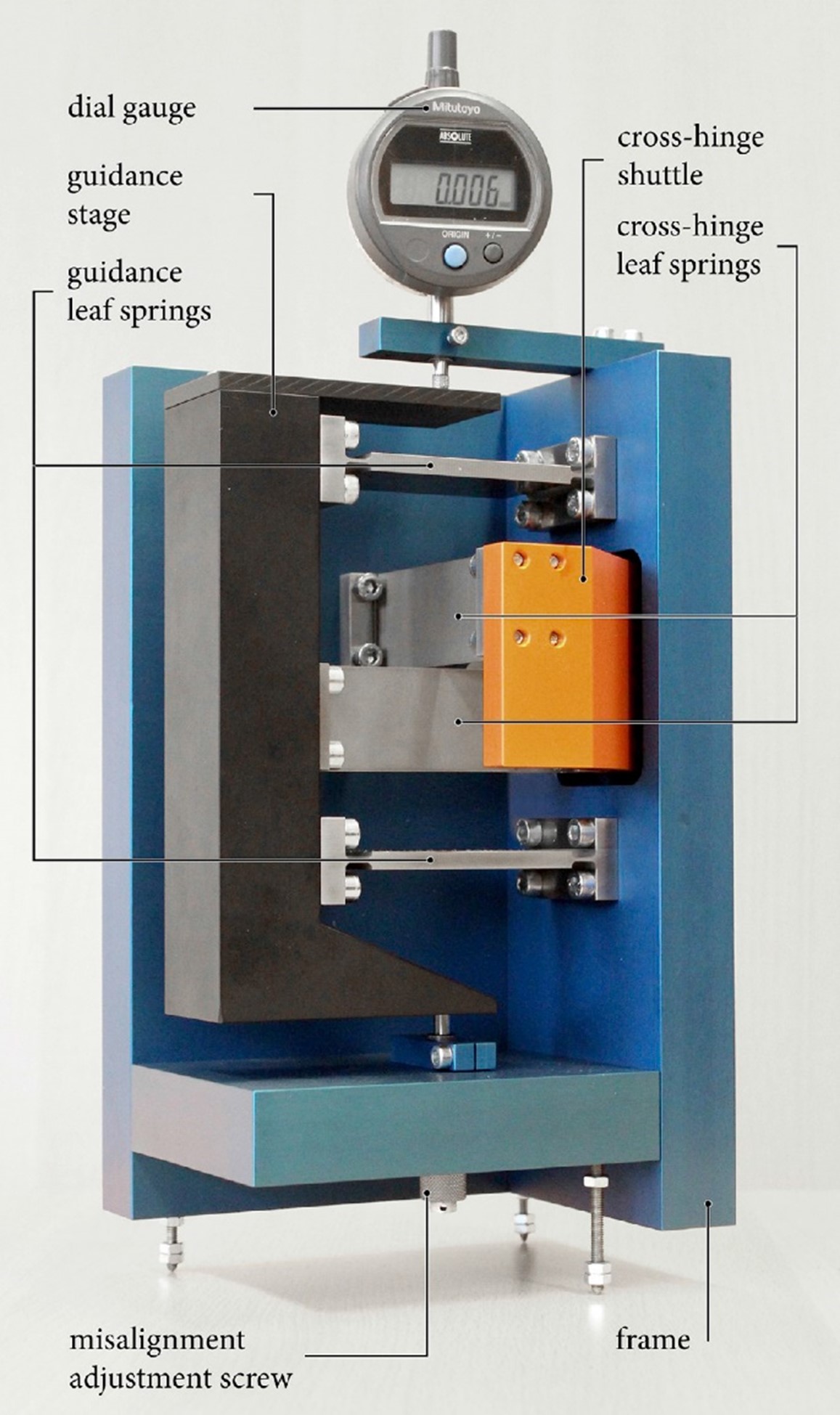
Allowable misalignments in an overconstrained flexure mechanism: The cross-hinge
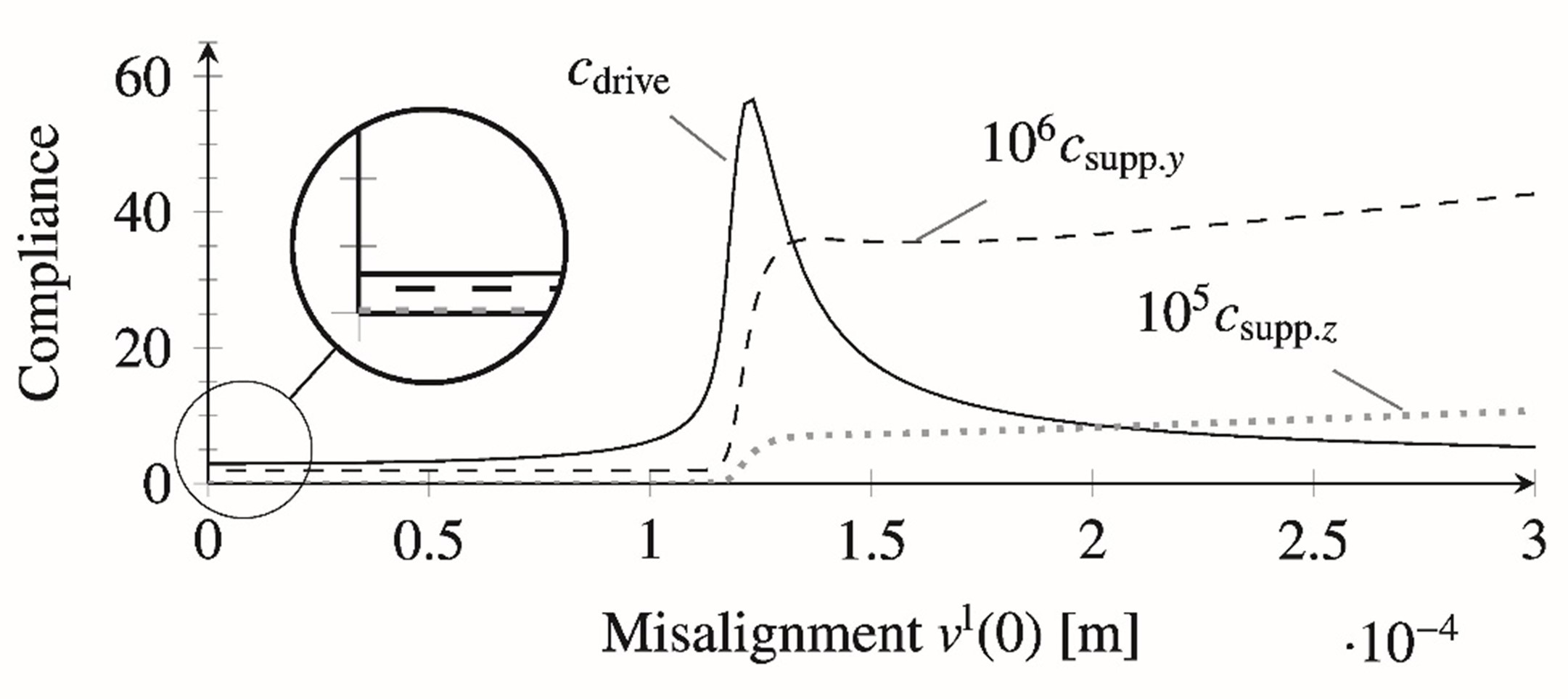
The exact-constraint design principle is commonly applied to flexure mechanisms to ensure deterministic behavior, but at the cost of reduced robustness, support stiffness, load capacity and usually an increased complexity of design. To explore the potential benefit of overconstrained design in flexure mechanisms, an elementary two-flexure cross-hinge with a single overconstraint serves as a case study. The stiffness effects of inadvertent stress due to misalignment are investigated experimentally, numerically and analytically. A measurement set-up with controllable misalignment has been designed. Measurements show that the first natural frequency of the cross-hinge decreases strongly with misalignment, suggesting that the actuation stiffness decreases due to the misalignment stress, and ultimately vanishes due to bifurcation buckling at a critical misalignment of the order of 0.1 mm for the mechanism at hand. Simulations with a detailed numerical model support the measurements and expose some additional factors, such as warping and shuttle compliance, which influence the system behavior. Importantly, they also show that the compliance in the support directions of the mechanism increases strongly at the critical misalignment, demonstrating that the mechanism no longer functions at the critical misalignment. An extensive analytical buckling analysis shows how the stress due to misalignment poses a functional operation limit on the overconstrained mechanism in terms of bifurcation buckling. The analysis serves to corroborate the numerical predictions. An expression is derived for the critical misalignment force and displacement as a function of the geometry and material of general cross-hinge mechanism designs.
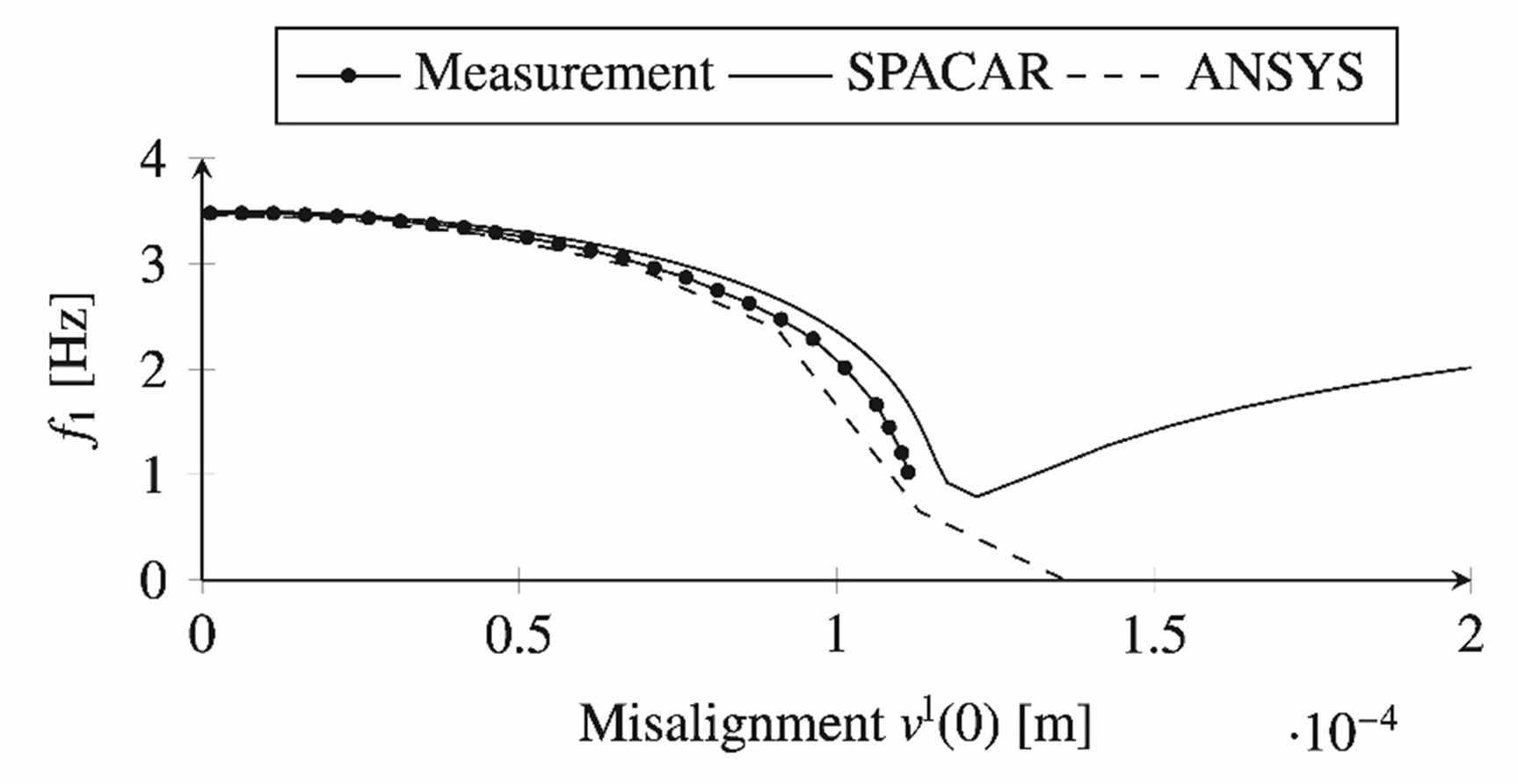 |
| Figure 4. First eigenfrequency as a function of misalignment, comparing measurement and numerical simulations. |
It is found that the practical ‘imperfections’ of shuttle elasticity, gravity and thickness variations only govern the smoothness of the transition from the fundamental path (of zero shuttle rotation) to the stable path after bifurcation. Without the imperfections, the transition is instant and sharp at the critical load; with imperfections, the transition is smoother. The imperfections do not affect the critical load or the post-buckling path markedly. The critical misalignment is increased by additional compliance in the experimental setup, most notably the compliance of the cross-hinge shuttle.
Principle
Overconstrained flexure design leads to strongly compromised static and dynamic behavior when a critical misalignment is reached. The results show that support stiffness suddenly drops a factor 19 to 275 when exceeding a certain critical misalignment angle. This critical angle can be approximated by [1]:
$$\frac{v_{cr}(L)}{L} \approx 14 \frac{t^2}{L^2}+4.6 \frac{t^2}{h^2}$$
When one can guarantee to stay within this critical limit of misalignment there is no stiffness or dynamics related objection to overconstrained design, which in turn facilitates higher support stiffness and load bearing capacity.
Developed by University of Twente
M. Nijenhuis, J.P. Meijaard, D.M. Brouwer
Referentie Bron
[1] Nijenhuis, M., Meijaard, J.P., Brouwer , D.M. (2019) Misalignments in an overconstrained flexure mechanism: A cross-hinge stiffness investigation, Precision Engineering, Volume 62, 2020, pp.181-195. https://doi.org/10.1016/j.precisioneng.2019.11.011
[2] J.P. Meijaard, D.M. Brouwer and J.B. Jonker, Analytical and experimental investigation of a parallel leaf spring guidance, Multibody System Dynamics (ISSN 1384-5640), 23(1), pp.77-97 (2010). DOI: 10.1007/s11044-009-9172-4