Chapter 2 - Design using flexures
Chapter 3 - Design for static stiffness
Allowable misalignment in an overconstrained flexure mechanism
The parallel leafspring mechanism
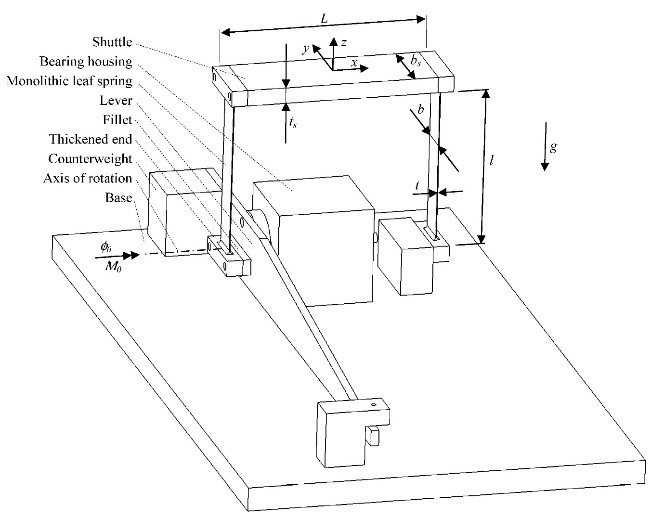
Statically determinate design is a principle than ensures predictable and repeatable behavior which is essential for precision mechanisms. However, the principle has certain potential drawbacks such as a lower support stiffness, compromised load bearing capacity, stress concentrations at attachments, and asymmetric and complex designs. The combination of static indeterminacy (overconstrained) and misalignment leads to difficult to predict and therefore unwanted behavior. The question how much misalignment can be tolerated. A parallel leafspring mechanism serves as a case study of a single overconstrained flexure mechanism. The overconstrained $\phi$-direction, is sensitive for rotational misalignment causing the stiffnesses to change suddenly. At the base of the left leafspring, shown in Figure 1, an adjustable misalignment in $\phi$-rotation is introduced by a lever attached to a hinged shaft. By adjusting the misalignment the influence on the dynamics can be experimentally researched. Spacar [1] flexible multibody software is used to numerically research the influence of the misalignment.
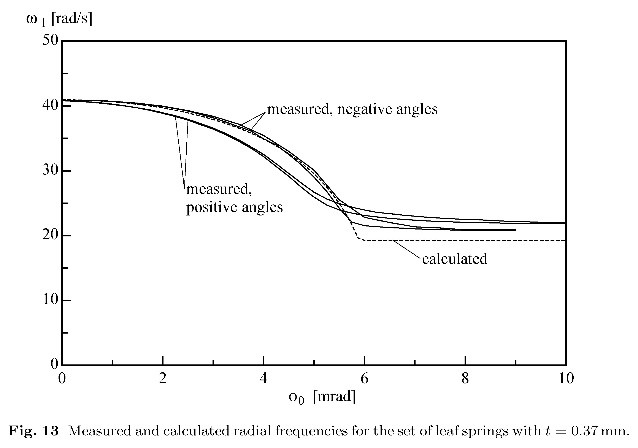 | 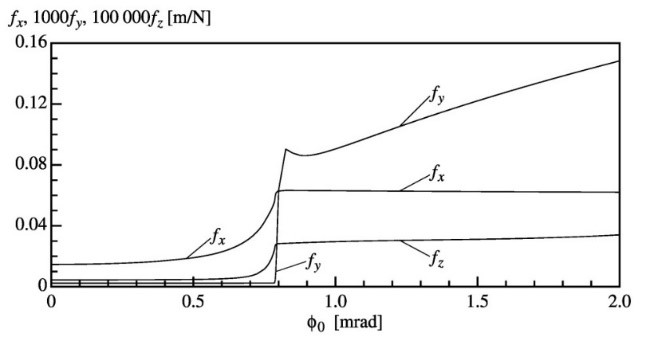 |
| Figure 3. Measured and calculated radial frequencies for a set of leafsprings with t = 0.37 mm. | Figure 4. Calculated compliances for the set of leaf springs with t = 0.20 mm. Note the scale factors. |
Figure 3 shows the gradual decrease of the first eigenfrequency with increasing misalignment. The critical misalignment angle is calculated to be 6.4mrad. This decrease in stiffness in the compliant direction is not disturbing, because this degree of freedom is usually controlled externally. Figure 4 shows the three translational compliances at the coordinate system shown in Figure 1. The critical misalignment angle is calculated to be 0.83 mrad. Clearly a lot of stiffness is lost when exceeding this misalignment angle. The decreased stiffness in the z- and especially in the y-direction is disturbing, because these are designed to be large to enhance precision manipulation. The negative effects of overconstrained design are largest if relatively thin and wide leaf springs are used. If misalignment angles are kept below 50% of the angle at which bifurcation occurs, overconstrained design of the parallel leaf spring mechanism is not significantly influencing the system natural frequencies and compliances. A qualitative agreement between theory and experiments is observed; differences can be explained by modelling idealizations and experimental imperfections.
Principle
Overconstrained flexure design leads to strongly compromised static and dynamic behavior when a critical misalignment is reached. The results show that especially the lateral stiffness (y-direction) drops suddenly when exceeding a certain critical misalignment angle. If the elastic pre-buckling displacements are neglected, the critical angle can be approximated by a lateral buckling moment Mcr according to Young et al. [2] , formulas for elastic stability, straight uniform beam under pure bending.
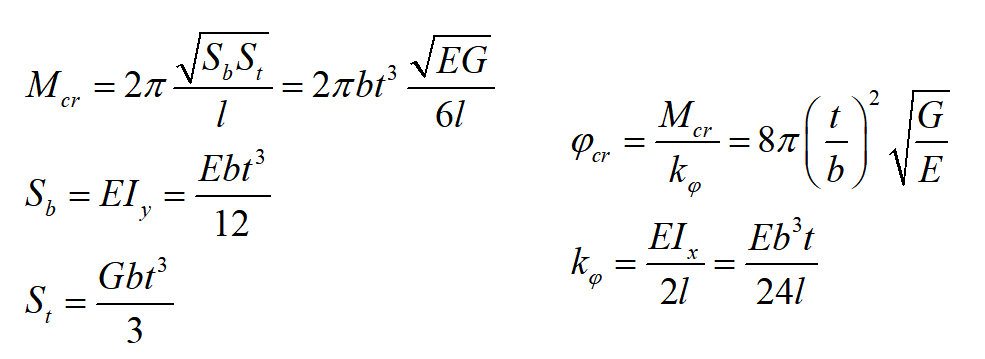
Overconstrained flexure design leads to strongly compromised static and dynamic behavior when a critical When one can guarantee to stay within this critical limit of misalignment there is no stiffness or dynamics related objection to overconstrained design, which in turn facilitates higher support stiffness and load bearing capacity.
Developed by University of Twente
- J.P. Meijaard, D.M. Brouwer
Referentie Bron
[1] J.B.Jonker and J.P. Meijaard “SPACAR — Computer Program for Dynamic Analysis of Flexible Spatial Mechanisms and Manipulators”. In: Multibody Systems Handbook Ed. by W. Schiehlen, 1990, pp.123-143.
[2] W.C. Young, R.G. Budynas, A.M. Sadegh, Roark’s formulas for stress and strain, McGraw Hill, New York, NY, 2012.
[3] J.P. Meijaard, D.M. Brouwer and J.B. Jonker, Analytical and experimental investigation of a parallel leaf spring guidance, Multibody System Dynamics (ISSN 1384-5640), 23(1), pp.77-97 (2010). DOI: 10.1007/s11044-009-9172-4