2.4.4 Net-radiation method
The Net-radiation method describes the radiosity balance of the different surfaces. Tracing of the exact source of the surface radiosity is not possible, but it can be used to calculated to balance in radiosity and the temperatures needed for this balance.
In most publications you can come across the following relation for the radiative heat flow from one surface to the other.
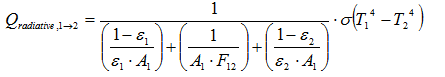
This is however not true. This is only the case for the net balance of radiosity (radiative exchange flux) between 2 surfaces that see only each other and nothing else (so basically they form an enclosure (i.e. F12 = 1).
In any other case the full network has to be solved to reach the net radiation imbalance for a node. The example below will show that otherwise one can make an huge error (in this case a factor 4).
This method uses the following definitions for radiation:
| Name | Symbol | Units | Description |
| Total emissive power $\varepsilon \cdot \sigma \cdot T^4$ | E | W/m2 | The rate at which radiation is emitted (per unit area) |
| Total irradiation | G | W/m2 | The rate at which radiation is incident (per unit area) |
| Total radiosity | J | W/m2 | The rate at which radiation leaves the surface (per unit area) |
This radiosity includes the reflected irradiated power, thus:
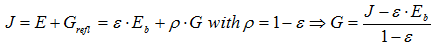
The net radiation:
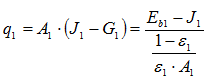
Now in the network these are two types of resistances.
Surface radiation resistance:
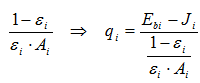
Geometrical radiative resistance:
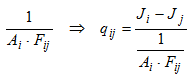
The main difference with this method compared to the Gebhart method is that the origin of the irradiation of a surface is not traceable.
