The choice for materials with a low Coefficient of Thermal Expansion (CTE) α is often proposed when dealing with such effects. Bending deformations caused by temperature gradients are often more significant than homogeneous expansion (or contraction). This means that not only the CTE is important, but also the thermal conductivity λ. The better the thermal conductivity, the smaller the temperature gradients and thus the bending deformation. In order for a structure to be insensitive to spatial temperature gradients, a material must be chosen with a high λ/α ratio.
When dealing with dynamical thermal disturbances, the thermal capacity also becomes important. The material properties that determine the thermal capacity are the density ρ and the specific heat cp. Different components in a structure, e.g. a metrology loop, will have different thermal capacities. Changes in temperature will cause dimensional changes of all components in the loop (errors). The components will react differently, unless they all cancel out around the metrology loop, which is unlikely in any situation involving dynamical temperature variations.
Besides the thermal capacity, also the thermal diffusivity is an important material property. The thermal diffusivity is defined as λ/(ρcp). A high thermal diffusivity means that a transient heat distortion is quickly spread out to a uniform temperature distribution. The sensitivity to thermal gradients and the thermal diffusivity can be combined to the characteristic λ/(αρcp), which expresses the capability of a material to maintain its shape due to temporal and spatial temperature variations. Material properties for some (typical) construction materials are shown in Figure 1.
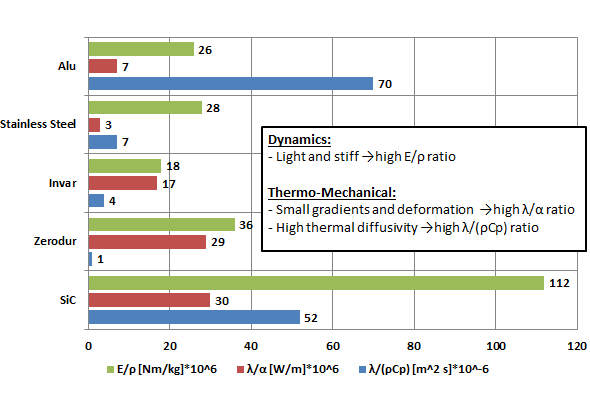
Figure 1: Material properties of typical construction materials
From the short outline above, it is clear that when dealing with thermal effects, not only the CTE is important, but also λ, ρ and cp. When dealing with thermal stresses, also the Young’s modulus E becomes important. This complicates material selection for thermal stability, compared to e.g. dynamics (vibration), where in most cases one only strives for a material with a high E/ρ ratio (specific stiffness).
