Balancing benefits and drawbacks

Fast-moving robots induce large dynamic reaction forces and moments at the base, resulting in vibrations and a loss of accuracy at the end-effector. By adding counter-masses and counter-inertias these shaking forces and moments may be reduced or even eliminated. In theory, this leads to a dynamic decoupling of the robot and its surroundings, reducing the vibration propagation and potentially eliminating the need for vibration isolation measures such as force frames, soft mounts, and active vibration isolation. In practice however, balancing leads to larger masses, increased motor torques and substantial bearing forces, since traditional balancing procedures rely on the addition of counter-masses. The addition of mass lowers the natural frequencies of the mechanisms leading to increased vibrations and a lowered controller bandwidth.

In this case study the trade-off between reduction of base vibrations and loss in controller bandwidth is studied on a scaled-down planar robot (Figure 1) that resembles an industrial delta-robot. The frequency response is investigated using an experimental set-up (Figure 2) and a flexible multi-body model in order to explain and quantify the effect of balancing on the shaking forces and controller performance of a finitely stiff manipulator. The influence of flexibility on the force-balancing quality of a planar delta-robot mechanism is assessed for three cases: 1) unbalanced, 2) fully force-balanced, 3) partially balanced.

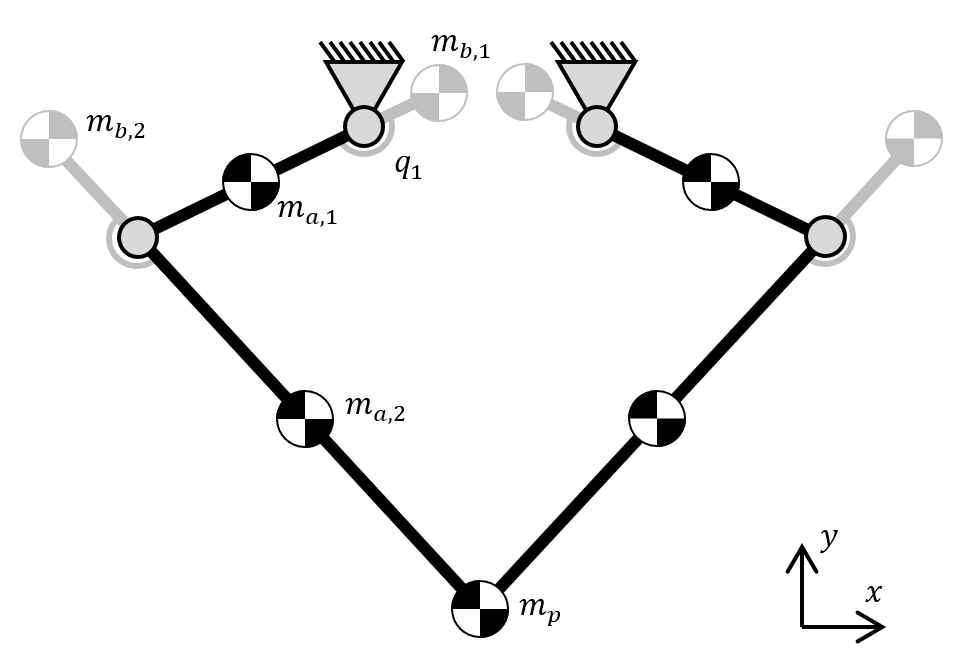Figure 1. The planar five bar mechanism with parameterization of force balance solution.	Figure 2. The force-balanced test set-up mounted on a 6-DoF force/torque sensor

A mechanism is shaking force balanced (or force balanced) when the total center of mass is stationary for all motion. A symmetric force balance solution with in-line counter-masses was chosen here. The large addition of mass can be mitigated by adopting a partial balance solution. Here, only counter-masses on the two upper links are used ($m_{b,2} = 0$). The location of the counter-masses is the same as for the previous case. The amount of added counter-mass ($m_{b,1}$), however, is lowered by 50%.

Two performance measures were used to evaluate the three cases. The first measure relies on the comparison of the transfer function matrix $T(s)$ from the actuator angles $q_1$ and $q_2$ to the shaking forces $F_x$ and $F_y$ at the base. The modelling outcomes and experimental results are shown in Figure 3. The second performance measure is the controller bandwidth, which is preferably high for disturbance suppression, accurate tracking and fast and precise positioning. In most applications the performance of the controller is limited by the first parasitic frequency as stability issues limit the controller bandwidth. In this case, balancing lowers the natural frequency of the system, from 28 to 19 Hz, indicating an approximate controller bandwidth loss of about 40%.

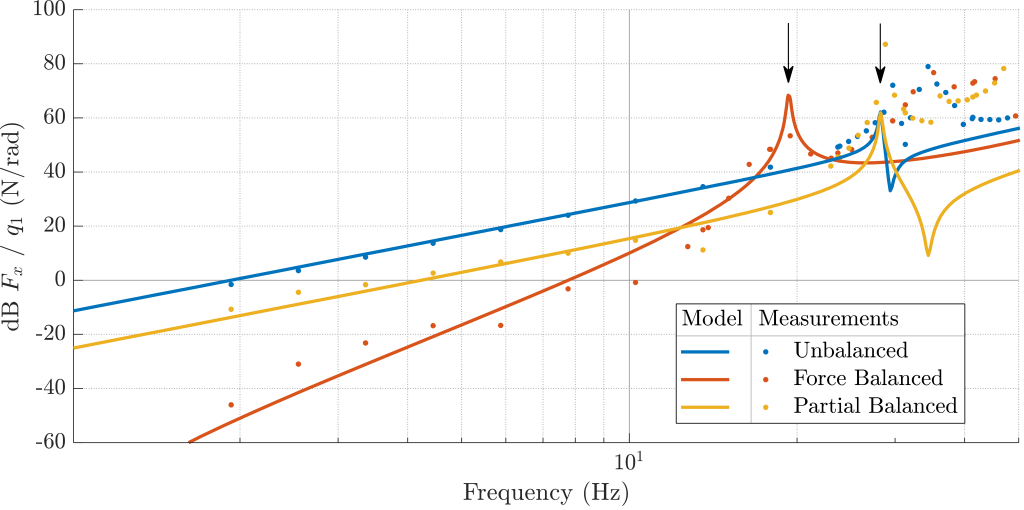
Figure 3. The shaking force frequency content of the 2-DoF mechanism in the horizontal x-direction due to actuation of joint 1. The dots indicate the results from the multisine identification. The back arrows indicate the first peaks due to the natural frequencies of the system.

For the fully force-balanced robot, the behavior corresponds to an 80 dB/decade line up to the first natural frequency at 19 Hz. The balanced and partially balanced systems have 2 masses and in the transfer therefore in general would have 2^nd and 4^th orders terms. In the specific case of the balanced system the 2^nd order vanishes. The partially balanced robot shares the 40 dB/decade line with the unbalanced mechanism. Yet, the magnitude of this line is significantly lower compared to the unbalanced case. Effectively, this results in approximately 15 dB or 80% reduction of the disruptive shaking forces in the frequency region below the first natural frequency.

Principle

Traditional balancing approaches disregard the elasticity of the robot links, which leads to undesirable parasitic dynamics, unbalance and loss of controller performance. It is demonstrated that a partial balancing solution accomplishes 80% shaking force reduction without the loss of controller bandwidth. The fully force balanced system has an approximate controller bandwidth loss of about 40%.

Developed by University of Twente

• J.J. de Jong, B.E.M. Schaars, D.M. Brouwer

Referentie Bron

[1] J.J. de Jong, B.E.M. Schaars, D.M. Brouwer (2019) The influence of flexibility on the force balance quality: a frequency domain approach. In Proceedings of the 19th international conference of the European Society for Precision Engineering and Nanotechnology (pp. 546-549).

[2] J.J. de Jong, B.E.M. Schaars, D.M. Brouwer (2020) Dynamic balance of finitely stiff mechanisms: Balancing benefits and drawbacks. Mikroniek, 2020(4), 40-44.