2.4.4.1 Numerical example
The Net-radiation method describes the radiosity balance of the different surfaces. Tracing of the exact source of the surface radiosity is not possible, but it can be used to calculated to balance in radiosity and the temperatures needed for this balance.
See the numerical example described in the Gebhart section
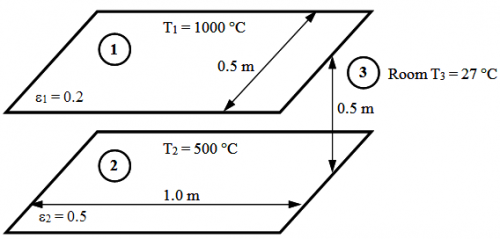
The resulting network representation:
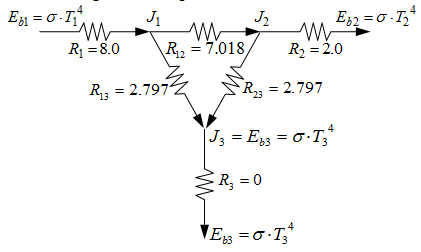
To solve the network, solve:
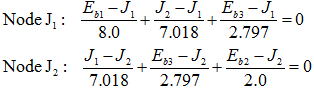
Where:
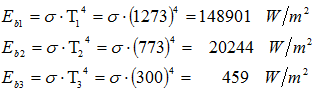
Solving the two equations

This results in;
The total heat loss by plate 1 is:
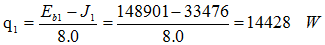
The total heat loss by plate 2 is:
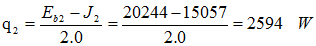
The total heat received by the room:
$q3={\Large\frac{J_1-J_3}{2.797} + \frac{J_2-J_3}{2.797} }= 17022\text{ } W$
Note: The heat-exchange between two surfaces cannot be solved directly with this method.
If the formula for a 2 surface enclosure is applied to this problem, the result would have been:
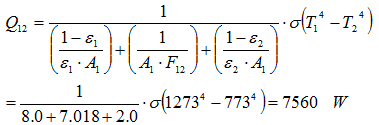
This is however not correct! This is only valid for a two surface enclosure. For more surfaces, the difference between the radiosities has to be calculated and therefore the total system of equations has to be solved.
The difference in radiative heat flux (radiosity) between the surfaces of both plates becomes:
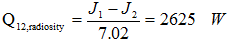
This is however not defined the same as the radiative heatflux in the Gebhart method. Which was found to be in the previous section:
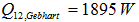
As can be seen the two methods do not give the same answer because their definition of radiative transfer is different.
Gebhart: Q12 means the radiative heatflux emitted by surface 1 and absorbed by surface 2 directly and through (possible) multiple reflections.
The net-radiation method does not track the origin of the radiation, but calculates the total radiative heatflux (radiosity) between surfaces (combination of emission and reflected incident radiation), without discrimination of its origin (thus also from other surfaces). The combined net heatflux of a surface shows the same result for both methods, thus the heatbalance remains correct for both methods.
The surface to surface heat transfer matrix (in W) of this system is given below for this method.

