2.4.3.2 Two surfaces facing each other
The Gebhart method describes the radiative heat transfer in terms of heat coming from one surface and absorbed by another, including all reflections. The Gebhart matrix traces exactly the radiative transfer contribution of each surface to the others.
For two flat surfaces close to each other, thus with a view factor close to 1 or when reflection via other surfaces can be neglected, the multiple reflections can be seen as a Taylor development and can therefore accurately be described by:

This results in the following relation for the radiative heat exchange, when only two surface are taken into account (no reflection via other surfaces assumed) of:
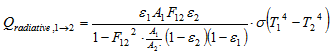
For two surfaces facing only each other (view factor of facing area = 1) this can even be simplified by:
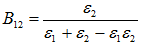
This relation is often used for ‘gap radiation’ and is the factor used in the model to get a first estimation of the radiative exchange between parts.
In many analyses the radiation factor Rij is used, which is the fraction (of the black body radiation) of radiation exchanged by two surfaces. This factor is defined as:
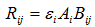
The radiative exchange factor matrix is a fully symmetrical matrix.
This leads to a heat transfer relation for each node of the following form:
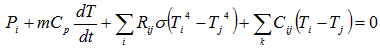
The radiative part in this relation can be linearised to an effective (temperature dependent) conductive factor in the following way:

This equivalent linearised conductance (Crad,12) is of course only valid for one combination of temperatures. If the temperatures are varying this equivalent ‘conductance’ should be update for each temperature step.
This linearised conduction is often also used in the form:
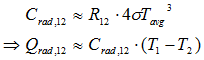
However one has to bear in mind that this relation is not exact and therefore should only be used in first order calculations.
