Ceramic laminate materials for combined high specific stiffness and damping

Although extensively studied, and heavily relied upon in machine tool design, material damping is difficult to quantify, and one must generally rely on empirical results. Often, the potential energy dissipation in a part is seriously restricted as the material is selected based on criteria other than damping. In fact, damping highly depends on alloy composition, frequency, stress history, level and type, (i.e., tension or shear), temperature, and joint preload.

Traditionally, cast iron was used in machine tools structures, having amplification-at-resonance factors $Q$ on the order of $10^2$. Subsequently, damping in polymer concrete materials was increased by a factor of 5 to 10. Despite the fact that the use of polymer concrete led to a marginal increase of machine weight and a decrease in thermal diffusivity, it is quite widely used for precision grinding machines.

Description

Design for high stiffness and damping usually implies a compromise. As indicated in Figure 1 [1] showing the stiffness-loss map for engineering materials, single phase materials have either high stiffness (structural metals and ceramics) or high damping (rubbery polymers), or a little of both (soft metals and hard plastics), and are typically below the line $|E^*|\tan \delta = 0.6 [GPa]$. This behavior is easily explained from the complex modulus notation $E^*=E^{‘}+jE^{”}=E^{‘} (1+j \eta) [GPa] $, where $E^{‘}$ is the storage or Young’s modules $E$, and $E^{”}$ is the loss modulus. High stiffness properties, usually coming from the real part of the complex modulus, automatically results in low loss factors $=\frac{E^{”}}{E^{‘}}=\tan \delta [-]$, and vice versa, low stiffness properties inherently imply high loss factors.

Instead of externally applying ‘unloaded’ elastic members to machine tool components, at the penalty of added moving mass (see tuned mass damping (TMD) and constrained layer damping (CLD)), viscoelastic damping materials can be embedded within the structural material itself, applying material composites such as reinforcements, sandwich materials and laminates. Ruzicka et al. found that as a result of the viscoelastic shear damping mechanism of polymers in structural composites, structural loss factors may be improved significantly [3].

Composite materials in general are assumed to have adhered layers and other combined components, such that no form of Coulomb or other type of slip is included as a damping contribution [4]. For composite materials (just as for adhesive bonded interfaces, as opposed to dry or lubricated interfaces in joints, which depending on the external load conceivably suffer from virtual play), the adhesive layer is a component part of the material system, and its stress, strain, and other rheological behavior can be analyzed in the same manner as other component (structural) parts of the composite. Thus, the damping analysis of the material composite generally requires a recognition of the individual components and a determination of the contribution of the total.

Metal matrix composite (MMC) materials improve damping properties considerably compared to single phase base materials. MMCs consist of chemically and physically different materials that are stir cast in a heterogeneous composition (matrix) with particles of about 10 $\mu m$ size. MMCs based on e.g. aluminum or magnesium, such as Mg2Si/Mg composites, feature low weight, high stiffness and strength and good vibration damping of up to 1% due to microscopic mechanism responsible for internal friction. The composites are typically used in automotive industry in powertrain components, brakes, bearing sleeves, and heat sinks.

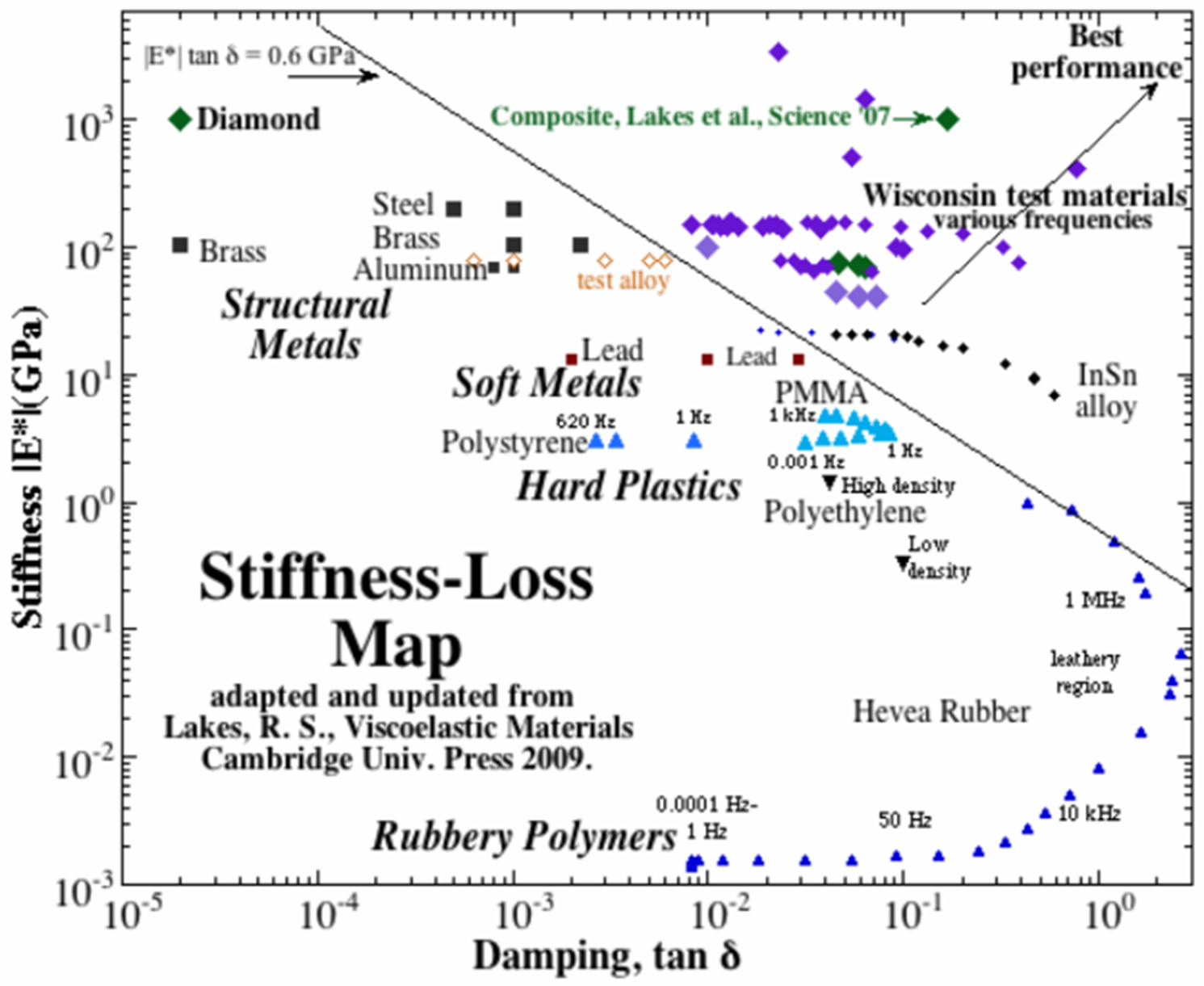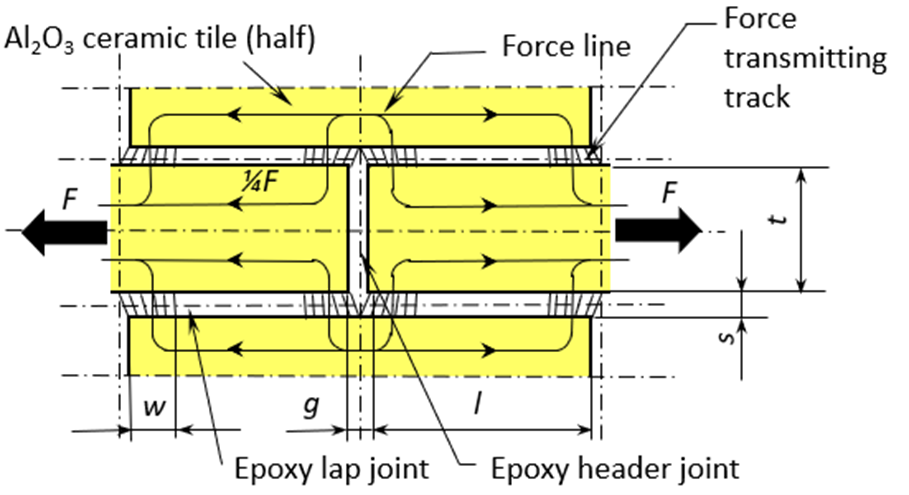Figure 1a. Stiffness-Loss map, adapted and updated from [1].	Ceramic-epoxy multi-layer laminate for high specific stiffness and damping [4].

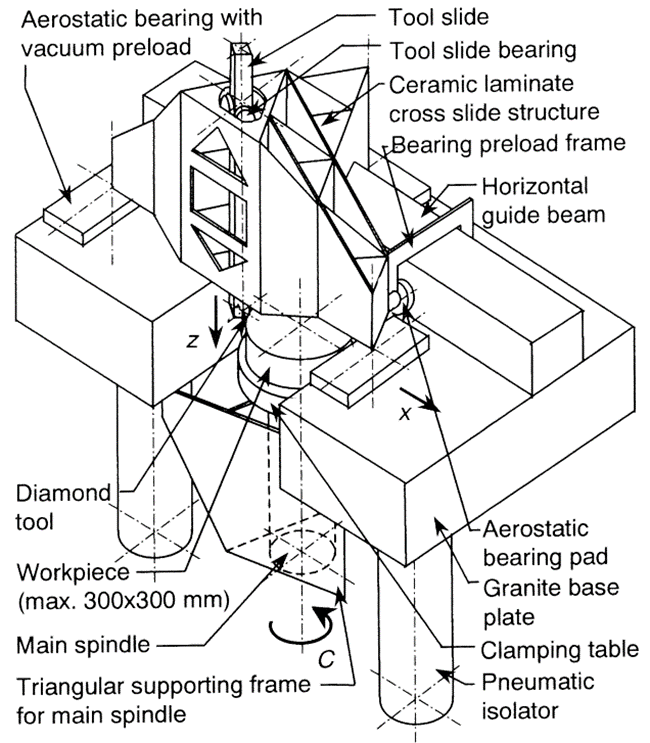
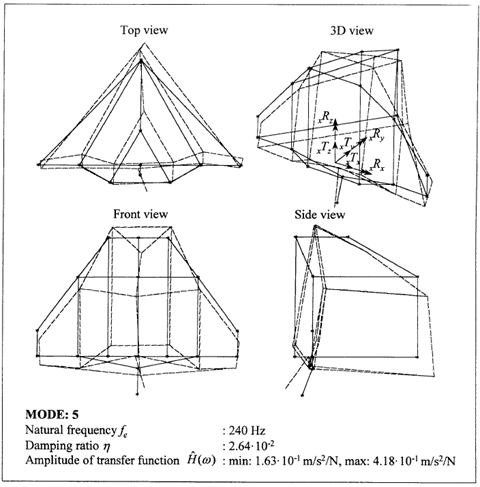
For concurrently yielding the profit in specific stiffness $\frac{E}{\rho}$ of ceramics and the viscoelastic shear damping mechanism of epoxy adhesives, a ceramic-epoxy multi-laminate material was proposed in for application in a single point diamond turning (SPDT) machine [5]. Alumina ceramic substrate tiles were used, mass produced via tape casing with dimensions of 2”x2”x0.025” and very high flatness of about 10 $\mu m$ and very high Al₂O₃ content >99.7%. Both experiments and analytical calculations on the multi-layer laminate materials displayed an increase in specific stiffness by a factor three compared to conventional structural materials, like steel and aluminum. Additionally, by using a laminate build-up, viscoelastic material damping was incorporated within the structural material itself [5], [6]. This as opposed to constrained layer dampers, where ‘statically unloaded’ elastic members (beams or plates) are used, which are attached in- or externally to machine tool components at the penalty of added mass. The structural loss factor $\eta_v$ of the epoxy resin adhesive amounts to about 6%, giving an overall structural loss factor $\eta_s$ of 3-4% as obtained from structural modal analyses (see Figure 4) [7]. The ceramic-epoxy laminate material offers extensive possibilities in design such as triangular build-up used here.

Figure 3. Schematic representation of single point diamond turning (SPDT) machine setup, with ceramic laminate cross slide structure [7].	Figure 4. Prototype realization of SPDT machine with sub-micron accuracy and optical surface quality (top), and mode shape analysis result on cross slide structure showing first internal mode at 240 Hz (bottom) [5], [7].

References

[1] Lakes, R.S., Viscoelastic materials, Cambridge University Press, 2009.

[2] Lakes, R.S., High Damping Composite Materials: Effect of Structural Hierarchy, Journal of composite materials, Vol. 36, No. 03/2002.

[3] Ruzicka, J.E., Derby, T.F., Schubert, D.W., Pepi, J.S., Damping of structural composites with viscoelastic shear-damping mechanisms, NASA CR-742 Contractor Report, Washington D.C., 1967.

[4] Lazan, B.J., Damping of materials and members in structural mechanics, Pergamon press, London, United Kingdom, 1968.

[5] Vermeulen, J.P.M.B, Ceramic Optical Diamond Turning Machine, Ph.D. Thesis, Eindhoven University of Technology, ISBN 90-5282-954-3, 1999.

[6] Vermeulen, J.P.M.B., Rosielle, P.C.J.N., Schellekens, P.H.J, Design rules for high stiffness ceramic laminate slide constructions, Structural geometry and material selection, 32nd CIRP International Seminar on Manufacturing Systems, Leuven, Belgium, pp. 135-145, 1999.

[7] Vermeulen, J.P.M.B., Rosielle, P.C.J.N., Schellekens, P.H.J., An advanced ceramic optical diamond turning machine – Design and prototype development, Journal: CIRP Annals – Manufacturing Technology, vol. 49, no. 1, pp. 407-410, 2000.

[8] Schellekens, P., et al, Design for precision: Current status and trends, Annals of the CIRP, Vol. 47/2, 1998.

Development

Hans Vermeulen, TU/e (1999)