Forced convection configurations
| Geometry | Validity range | Relation | Reference* |
| Flat plate, laminar | Re<5E5 Pr>0.5 | Pohlhausen | Bejan, 5.82 |
| Flat plate, turbulent | 5e5<Re<1E8 Pr>0.5 | Colburn | Bejan, 5.134 |
| Internal pipe flow, laminar | Re<3000 | Bejan, 6.32, table 6.2 | |
| Internal pipe flow, turbulent | 0.5<Pr<2000 Re>3000 | Dittus-Boelter | Bejan, 6.90 |
| Internal pipe flow, turbulent | 0.7<Pr<16700 Re>1E4 L/D>10 | Sieder-Tate | Bejan, 6.91 |
| Cylinder in external cross flow | 7E4<Re<4E5 | Churchill/Bernstein | Bejan, 5.135 |
| Sphere | 3.5<Re<7.6E4 0.71<Pr<380 | Whitaker | Bejan, 5.139 |
| General body, external flow | 0<Re< 2E5 Pr>0.7 | Yovanovich | Bejan, 5.142 |
*The references to the formulas refer to Bejan, “Heat Transfer: Evolution, Design and Performance”, 2022.
Flat plate, laminar forced flow
The heat transfer from a plate to a laminar flow varies greatly with position in the flow direction, so the relation below is an average Nusselt value for a plate of length L. Transition to turbulence for this geometry occurs at roughly ReL>5E5, at which point a different correlation is needed.
$$\overline{{Nu}_{L}} = 0.664 Pr^{1/3} Re_{L}^{1/2}$$
Flat plate, turbulent forced flow
Turbulence greatly increases the heat transfer between a fluid and a surface, due to the much stronger mixing in the fluid. Again, The Nusselt number (and heat transfer) will vary along the length of the plate. The correlation given here gives a average value of Nu for a plate of length L in the flow direction:
$$\overline{{Nu}_{L}} = 0.037 Pr^{1/3} (Re_{L}^{4/5} – 23.550)$$
Internal pipe flow, laminar
The Nusselt number for laminar, fully developed pipe flow is a constant, dependent only on the duct cross-section. Note that this is the case only for fully developed flow, past a certain entrance length X, typically defined in terms of pipe diameter D (or, Dh) as:
$$X = \frac{D}{20} Re_{D}$$
So the following table holds for pipes in which L>>X:
| Cross section | Friction factor f*ReDh | NuDh (uniform heat flux) | NuDh (isothermal wall) |
| Circle | 16 | 4.364 | 3.66 |
| Square | 14.2 | 3.63 | 2.89 |
| Equilateral triangle | 13.3 | 3 | 2.35 |
| Rectangle (1:4) | 18.3 | 5.35 | 4.65 |
| Parallel plates | 24 | 8.235 | 7.54 |
Note that here, Nu is based on Dh as the length scale; that is, the hydraulic diameter as defined earlier in this section. The listed friction factor is important in determining flow speed in a pipe. Usually this is done using the Darcy-Weisbach equation. This is will not be discussed here, but plenty of information can be found online.
Internal pipe flow, turbulent, low temperature difference
The nusselt number for a turbulent flow through a pipe can easiest be described by the Dittus-Boelter equation. This equation is an explicit function, which makes it easy to solve, but may be less accurate if there is a large gradient across the fluid.
$$Nu = 0.027 Re^{4/5} Pr^{n}$$
Where n = 0.4 for the fluid being heated and n = 0.3 for the fluid being cooled.
Internal pipe flow, turbulent, general
The Sieder-Tate relation is more accurate than the Dittus-Boelter relation, but it is implicit, because of the correction of the viscosity, which will change as the Nusselt number changes. This means that it must be solved iteratively to converge towards a value for Nu.
$$Nu = 0.027 Re^{4/5} Pr^{1/3} \frac{\mu}{\mu_{s}}$$
In which μ is the viscosity at the bulk fluid temperature and μs is the viscosity at the heat transfer boundary temperature
Cylinder in external cross flow
For a long cylinder oriented across a fluid stream one correlation that is based on data from many independent sources is:
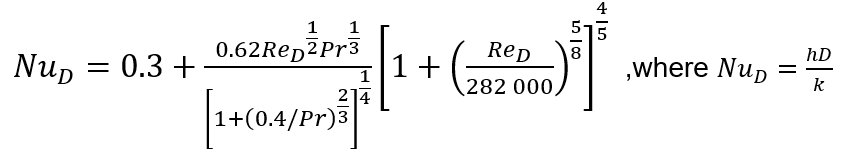
This formula holds for all values of ReD and Pr, provided the Péclet number PeD = ReDPr is greater than 0.2.
Sphere
For a sphere in an isothermal free stream Whitaker proposed the equation:
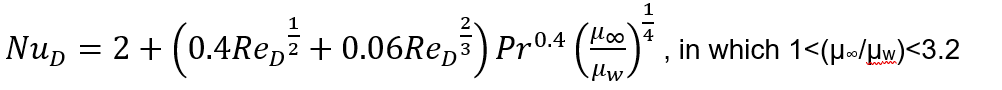
All the physical properties are evaluated at the free-stream temperature T∞, except μw, which is the viscosity evaluated at the surface temperature, μw = μ(Tw). The no-flow limit of this formula (NuD=2), agrees with the pure conduction for a steady conduction in a motionless medium
General body in external flow
For bodies of other shapes Yovanovich proposed a universal equation (for spheroids). As length scale for the definition of the Reynolds and Nusselt numbers, Yovanovich chose the square root of the spheroid surface A for the characteristic length L:
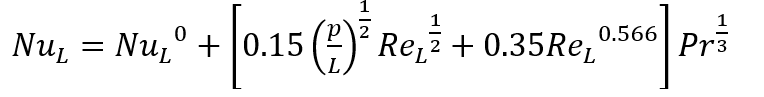
where p is the maximum (equatorial) perimeter of the spheroid, in the plane perpendicular to the flow direction. The constant NuL0 is the overall Nusselt number (near 3.5) in the no-flow condition.
